
141.单向链表是否有环
假如该链表是循环链表,那我们可以定义两个指针,一个每次向前移动两个节点,另一个每次向前移动一个节点。这就和田径比赛是一样的,假如这两个运动员跑的是直道,那快的运动员和慢的运动员在起点位于同一位置,但快的运动员必将先到达终点,期间这两个运动员不会相遇。而如果绕圈跑的话(假设没有米数限制),跑的快的运动员在超过跑的慢的运动员一圈的时候,他们将会相遇,此刻就是循环链表。
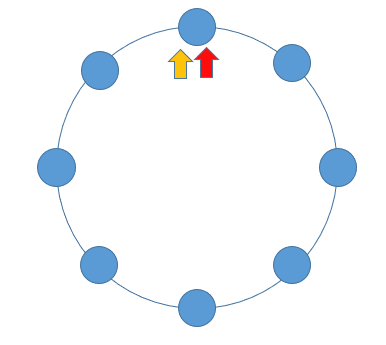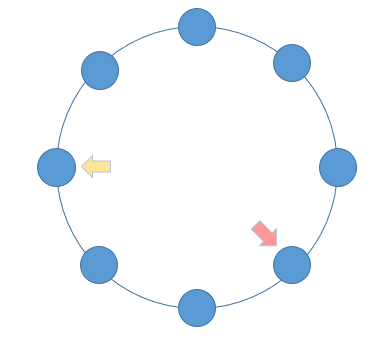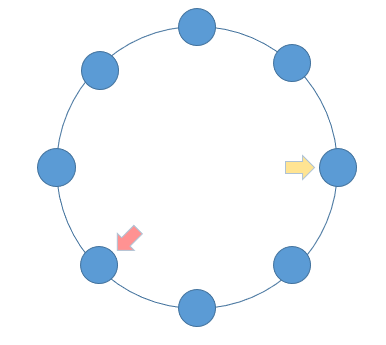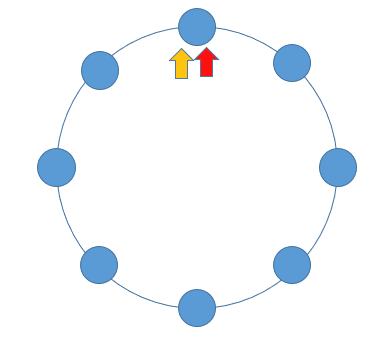
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head == NULL || head->next == NULL) {return false;}
ListNode* slow = head;
ListNode* fast = head;
while(fast->next!=NULL && fast->next->next!=NULL) {
slow = slow->next;
fast = fast->next->next;
if(slow == fast) {
return true;
}
}
return false;
}
};
141.单向链表环入口
从链表头节点开始,快慢指针同时开始移动,快指针每次移动2,慢指针每次移动1,若快指针最终与慢指针相遇,则表示链表有环,否则,则为无环。
有环情况下,快慢指针相遇时,慢指针位置不变,将快指针置回表头,步长改为每次移1,快慢指针同时开始移动,再次相遇处即为环的入口。
⬇️<-<-<-⬆️
⬇️ ⬆️
♦️->->->⬇️->->->⬆️
A B C
♦️也就是A的位置是头节点,B表示环入口处,C表示快慢指针第一次相遇处。
在C处相遇时,设慢指针跑了N步,也就是从A开始N步后会到达C。
快指针比慢指针走的快一倍,也就是走了2*N步。那么慢指针从C处再跑N步还会回到C处。
既然都会回到C处,那么必然会在B点第一次相遇。
所以我们在入口处再设一指针(用之前快指针即可),与慢指针用1步长同时前进,第一次相遇处就是环入口处。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if(head == NULL || head->next == NULL ) {return NULL;}
ListNode* slow = head;
ListNode* fast = head;
while(fast->next && fast->next->next) {
slow = slow->next;
fast = fast->next->next;
if(slow == fast) {
fast = head;
while(fast != slow) {
fast = fast->next;
slow = slow->next;
}
return fast;
}
}
return NULL;
}
};