
题目描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/combination-sum
思路
根据示例 1:输入: candidates = [2,3,6,7],target = 7。
- 候选数组里有 2 ,如果找到了 7 - 2 = 5 的所有组合,再在之前加上 2 ,就是 7 的所有组合;
- 同理考虑 3,如果找到了 7 - 3 = 4 的所有组合,再在之前加上 3 ,就是 7 的所有组合,依次这样找下去;
- 上面的思路就可以画成下面的树形图。
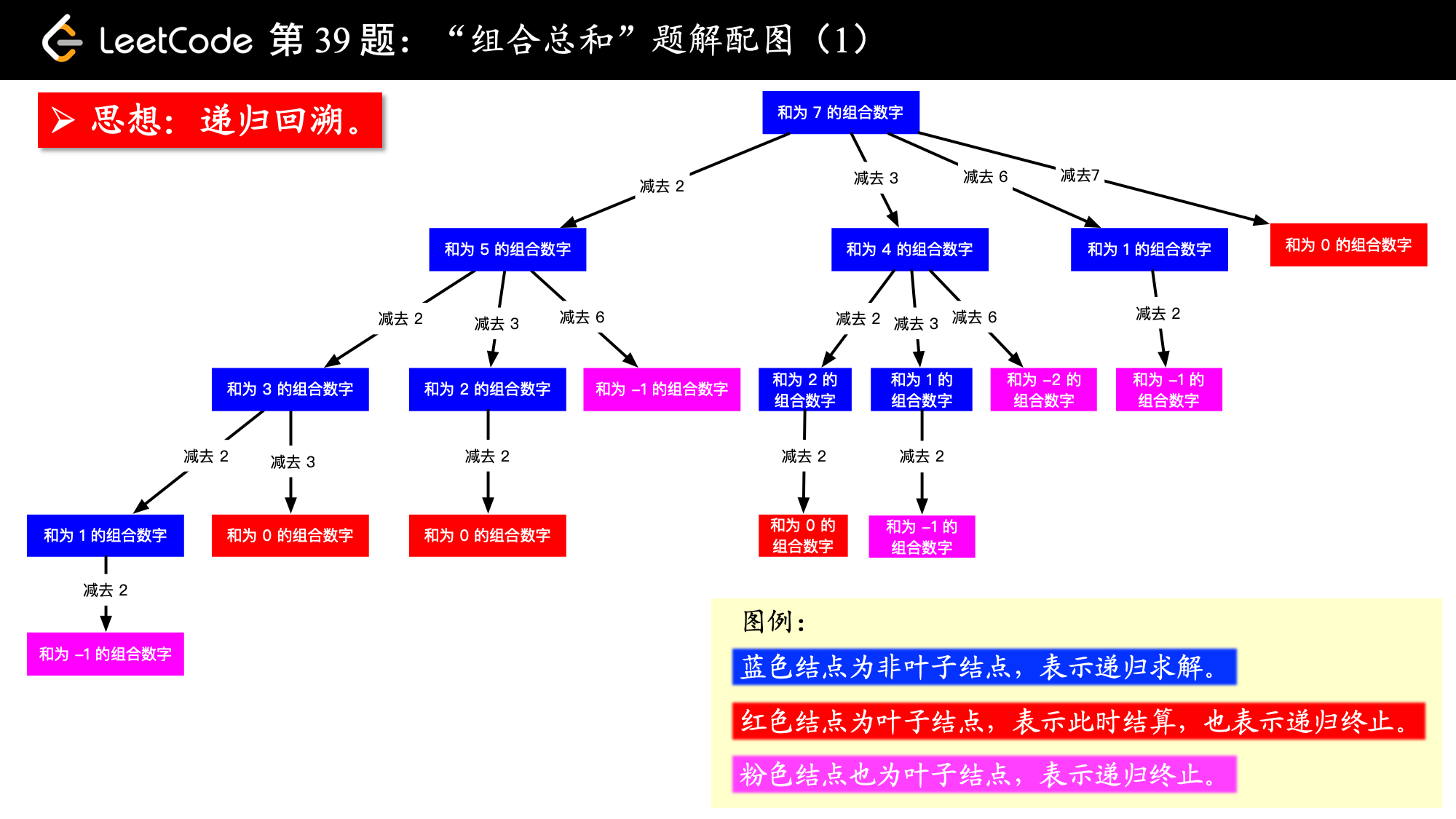
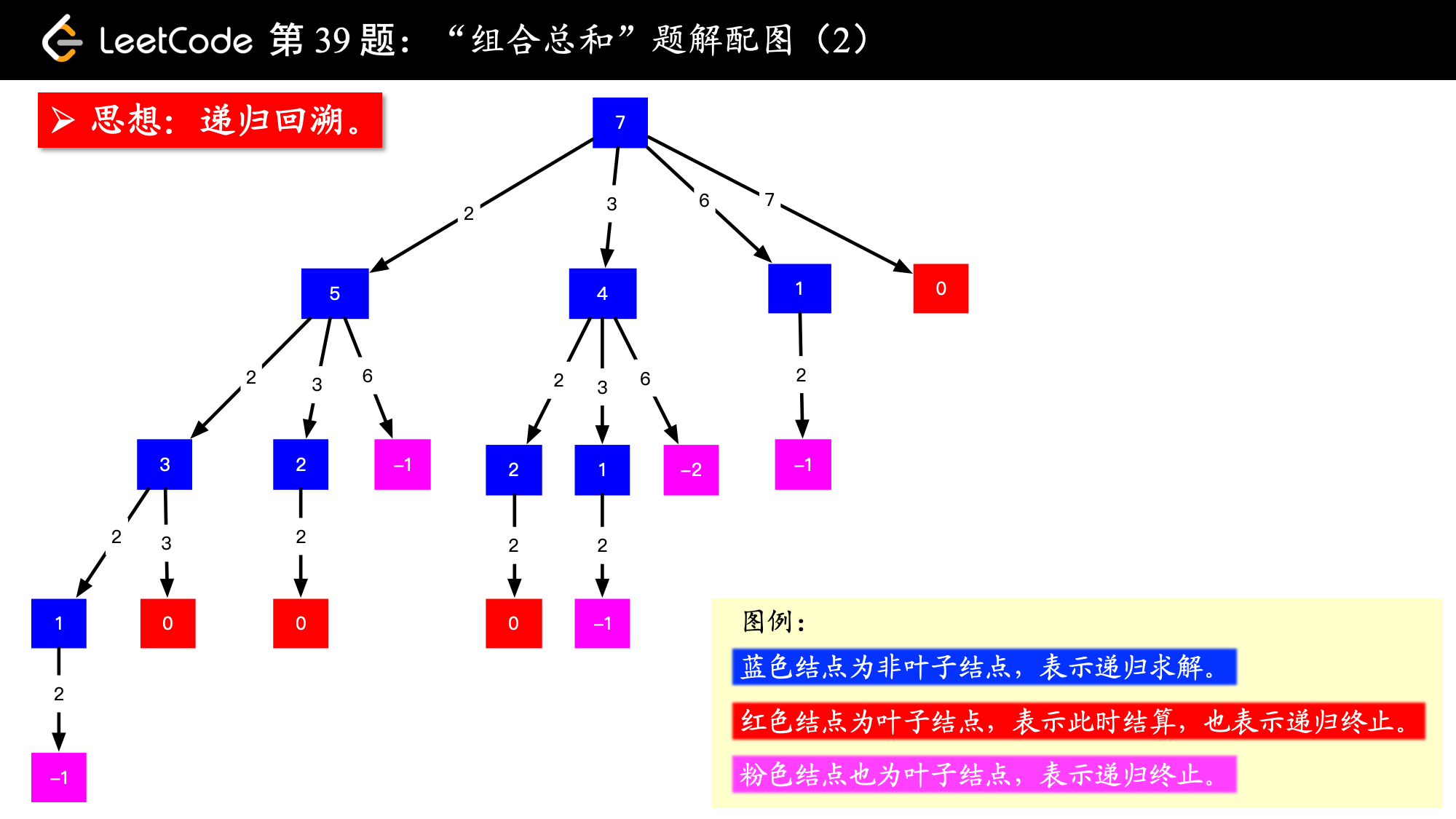
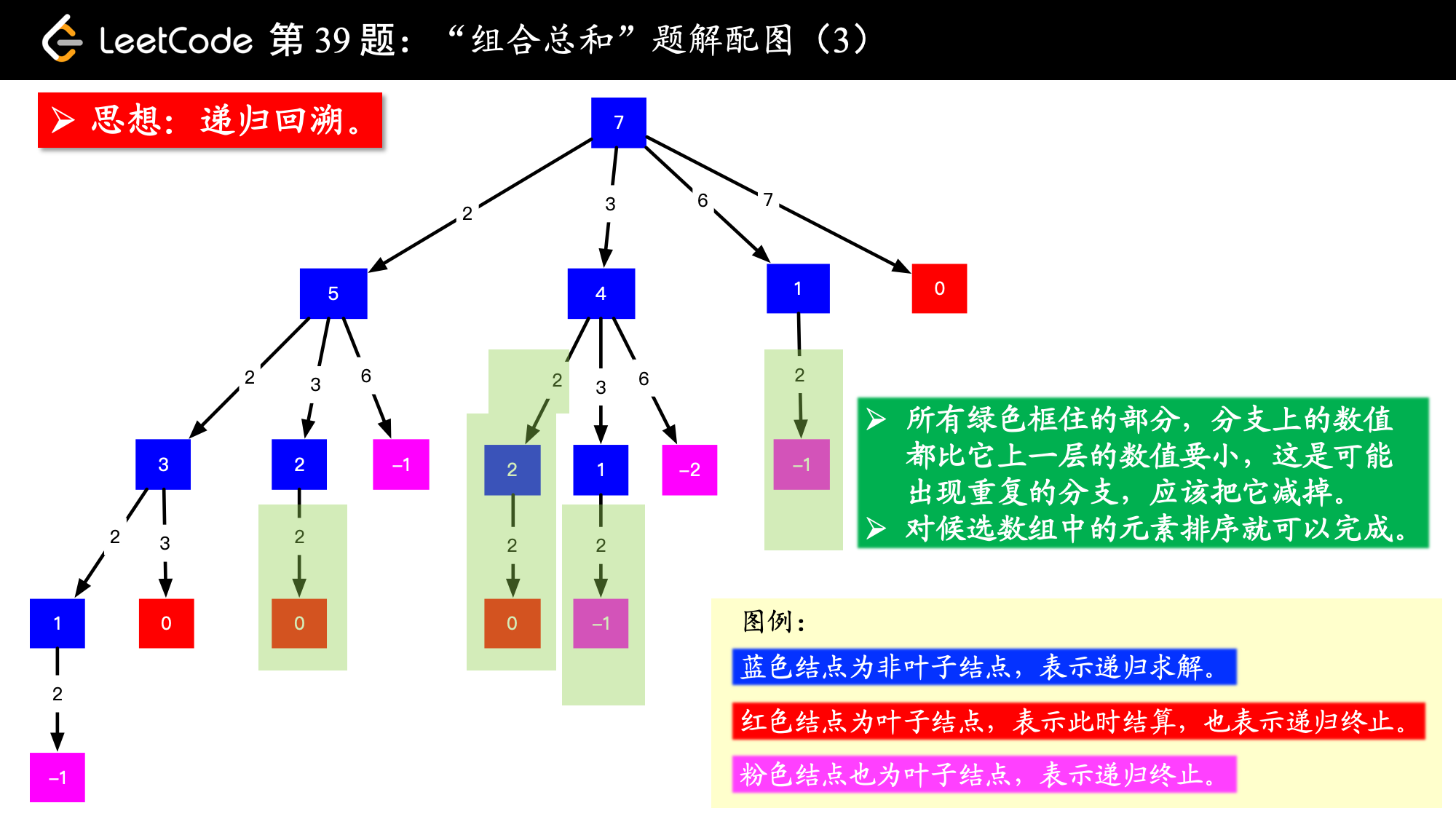
画出图以后,我看了一下,我这张图画出的结果有 4 个 0,对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]],而示例中的解集只有 [[7], [2, 2, 3]],很显然,重复的原因是在较深层的结点值考虑了之前考虑过的元素,因此我们需要设置“下一轮搜索的起点”即可.
- 去重复
- 在搜索的时候,需要设置搜索起点的下标 begin ,由于一个数可以使用多次,下一层的结点从这个搜索起点开始搜索;
- 在搜索起点 begin 之前的数因为以前的分支搜索过了,所以一定会产生重复。
- 剪枝提速
-
如果一个数位搜索起点都不能搜索到结果,那么比它还大的数肯定搜索不到结果,基于这个想法,我们可以对输入数组进行排序,以减少搜索的分支;
-
排序是为了提高搜索速度,非必要;
-
搜索问题一般复杂度较高,能剪枝就尽量需要剪枝。把候选数组排个序,遇到一个较大的数,如果以这个数为起点都搜索不到结果,后面的数就更搜索不到结果了。
-
-
 “ 半角空格” -
 “ 全角空格” <br>换行
代码
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
void DFS(int start,int target,vector<int> candidates)
{
if (target == 0) {
ans.push_back(path);
return;
}
for(auto i = start;i<candidates.size() && target-candidates[i]>=0;i++) {
path.push_back(candidates[i]);
DFS(i,target-candidates[i],candidates);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target)
{
sort(candidates.begin(),candidates.end());
DFS(0,target,candidates);
return ans;
}
};